RWA#1: Unit M Concepts 4-6: Conic Sections in real life

1.  An ellipse is the set of all points such that the sum of the distance from two points (which is the foci) is constant.

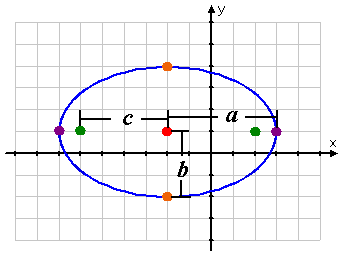
2.    To find the ellipse itself, it has to be in standard conic form which is (x-h)^2/a^2+ (y-k)^2/b^2 = 1. It doesn't matter where a^2 and b^2 are, they can be under either one. But one thing that always has to stay the same is where h and k are. H must always be with x and k must always be with y. Also to determine the size of the ellipse, whether it's skinny or fat, will be based on "x" or "y". If the bigger number is under "x" then it's fat, but if it's under "y" then it's skinny.
    When its graphed h,k will be our center points. What ever numbers are in the the denominators place, the biggest number will be "a" and the second one "b". We get our vertices from "a", co-vertices from "b", and our foci from "c". If "a" has our bigger numbers then it's our major axis and "b" will determine our minor axis. The foci will be on the major axis but a couple of points before it reaches the vertices points. To determine the eccentricity of an ellipse, the formula is e = c/a. So it's whatever number is "c" divided by whatever number "a" is.
  



3.  One place that ellipses can be found in the real world is in the medical field. Extra corporeal Shock wave Lithotripsy is a new medical treatment that can decrease the size of kidney and gall stones in people. A patient can be placed next to a machine that "shock waves away from the patient and into an elliptical bowl" (http://www.purplemath.com/modules/ellipse.htm). The patient is well positioned so that the gall stone is at one focus with the elliptical bowl. When the machine emits the shock wave from the other focus, the waves scatter to the elliptical bowl, bounce from that and to the other focus. When it reaches the other focus, the wave is at full power.
    So that type medical science can treat patients well out surgery and the patient itself can leave that same day. The shock wave smashed the stones so that the body can get rid of them more easily. Math and medical science come together for the beneficial purpose of helping people.

4.   References: 
    http://www.purplemath.com/modules/ellipse.htm
    http://www.lessonpaths.com/learn/i/unit-m-conic-sections-in-real-life/conic-sections-in-real-life
    http://www.youtube.com/watch?v=lvAYFUIEpFI